Diskret funktion vs kontinuerlig funktion
Funktioner er en af de vigtigste klasser af matematiske objekter, som i vid udstrækning bruges i næsten alle underfelter i matematik. Som deres navne antyder, er både diskrete funktioner og kontinuerlige funktioner to specielle typer funktioner.
En funktion er en relation mellem to sæt defineret på en sådan måde, at for hvert element i det første sæt er den værdi, der svarer til det i det andet sæt, unik. Lad f være en funktion defineret fra sæt A til sæt B. For hver x ϵ A angiver symbolet f (x) den unikke værdi i sæt B, der svarer til x. Det kaldes billedet af x under f. Derfor er en relation f fra A til B en funktion, hvis og kun hvis for, hver xϵ A og y ϵ A; hvis x = y, så er f (x) = f (y). Sæt A kaldes domænet for funktionen f, og det er det sæt, hvor funktionen er defineret.
Overvej for eksempel forholdet f fra R til R defineret af f (x) = x + 2 for hver xϵ A. Dette er en funktion, hvis domæne er R, som for hvert reelle tal x og y, x = y betyder f (x) = x + 2 = y + 2 = f (y). Men forholdet g fra N til N defineret af g (x) = a, hvor 'a' er en primærfaktor for x, er ikke en funktion som g (6) = 3, såvel som g (6) = 2.
Hvad er en diskret funktion?
En diskret funktion er en funktion, hvis domæne højst kan tælles. Simpelthen betyder det, at det er muligt at oprette en liste, der indeholder alle elementerne i domænet.
Ethvert endeligt sæt kan højst tælles. Sættet med naturlige tal og sættet med rationelle tal er eksempler på højst utallige uendelige sæt. Sættet med reelle tal og antallet af irrationelle tal kan højst ikke tælles. Begge sæt er utallige. Det betyder, at det er umuligt at oprette en liste, der indeholder alle elementerne i disse sæt.
En af de mest almindelige diskrete funktioner er faktorfunktionen. f: NU {0} → N rekursivt defineret af f (n) = nf (n-1) for hver n ≥ 1 og f (0) = 1 kaldes faktorfunktionen. Vær opmærksom på, at dens domæne NU {0} højst kan tælles.
Hvad er en kontinuerlig funktion?
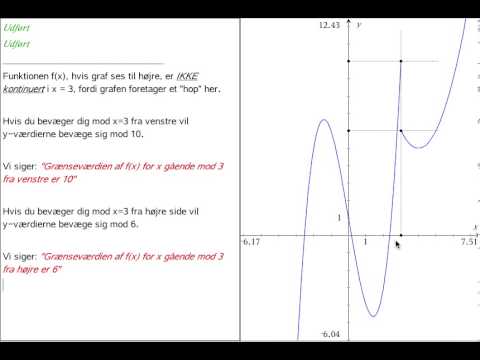
Lad f være en funktion således, at for hver k i domænet f, f (x) → f (k) som x → k. Så er f en kontinuerlig funktion. Dette betyder, at det er muligt at gøre f (x) vilkårligt tæt på f (k) ved at gøre x tilstrækkeligt tæt på k for hver k i domænet f.
Overvej funktionen f (x) = x + 2 på R. Det kan ses, at som x → k, x + 2 → k + 2, der er f (x) → f (k). Derfor er f en kontinuerlig funktion. Overvej nu g på positive reelle tal g (x) = 1 hvis x> 0 og g (x) = 0 hvis x = 0. Derefter er denne funktion ikke en kontinuerlig funktion, da grænsen for g (x) ikke findes (og derfor er det ikke lig med g (0)) som x → 0.
Hvad er forskellen mellem diskret og kontinuerlig funktion?
• En diskret funktion er en funktion, hvis domæne højst kan tælles, men det behøver ikke være tilfældet i kontinuerlige funktioner.
• Alle kontinuerlige funktioner ƒ har den egenskab, at ƒ (x) → ƒ (k) som x → k for hver x og for hver k i domænet ƒ, men det er ikke tilfældet i nogle diskrete funktioner.